一些学习中遇到的数学知识

数学

数学是基础，线代更是。

范数

花书24页

范数，是具有“长度”概念的函数。在线性代数、泛函分析及相关的数学领域，范数是一个函数，是矢量空间内的所有矢量赋予非零的正长度或大小。半范数可以为非零的矢量赋予零长度。

定义范数的矢量空间是赋范矢量空间；同样，定义半范数的矢量空间就是赋半范矢量空间。

**注：**在二维的欧氏几何空间 R中定义欧氏范数，在该矢量空间中，元素被画成一个从原点出发的带有箭头的有向线段，每一个矢量的有向线段的长度即为该矢量的欧氏范数。

线性相关

在线性代数里，矢量空间的一组元素中，若没有矢量可用有限个其他矢量的线性组合所表示，则称为线性无关或线性独立 [1] (linearly independent)，反之称为线性相关(linearly dependent)。

例如在三维欧几里得空间R的三个矢量(1, 0, 0)，(0, 1, 0)和(0, 0, 1)线性无关；但(2, −1, 1)，(1, 0, 1)和(3, −1, 2)线性相关，因为第三个是前两个的和。

1、向量a1,a2, ···,an(n≧2)线性相关的充要条件是这n个向量中的一个为其余(n-1)个向量的线性组合。

2、一个向量线性相关的充分条件是它是一个零向量。

3、两个向量a、b共线的充要条件是a、b线性相关 [2] 。

4、三个向量a、b、c共面的充要条件是a、b、c线性相关。

5、n+1个n维向量总是线性相关。【个数大于维数必相关】

矩阵列空间

线性空间 / 向量空间

向量空间又称线性空间，是线性代数的中心内容和基本概念之一。在解析几何里引入向量概念后，使许多问题的处理变得更为简洁和清晰，在此基础上的进一步抽象化，形成了与域相联系的向量空间概念。譬如，实系数多项式的集合在定义适当的运算后构成向量空间，在代数上处理是方便的。】单变元实函数的集合在定义适当的运算后，也构成向量空间，研究此类函数向量空间的数学分支称为泛函分析。

向量空间它的理论和方法在科学技术的各个领域都有广泛的应用。

欧氏空间

参考 https://www.zhihu.com/question/27903807?sort=created

可以理解为维度大于3的向量空间

齐次点坐标

参考 https://wenku.baidu.com/view/a3d35eec81c758f5f61f6709.html

一维齐次坐标点

定义1

设欧氏直线上有穷远点$p$的笛氏坐标为$x$ , ,则满足气 $ \frac{x_1}{x_2}=x$的两数$ x_1,x_2 (x_2≠0)$叫做点$p$的齐次(笛氏)坐标，记作$p(x,x) ,x$称点$p$的非齐次坐标.

如：若(2, 1)是齐次点坐标，则它的非齐次坐标为(2)，反之成立。

如果$x≠0,x2=0$，则$p(x_1,0)$或$p(1,0)$为轴上的无穷远点。

证明：

任取一点$p(x)$，它的齐次坐标为$p(x,1)$ 或$p(1,\frac{1}{x})$，当$x→∞$时，$p→p_\infty$，此时$(1,\frac{1}{x})\to(1,0)$。因此，轴上的无穷远点为点$(x,0)$或$(1,0)$。

• 要特别注意，无穷远点没有非齐次坐标.
• 如果点的非齐次坐标存在，则它就是唯一的.
• 对于轴上的任何(有穷或无穷远点，它的齐次坐标无穷多组.

二维齐次坐标点

定义2：

设欧氏平面内点$p$的笛氏坐标为$(x.y)$，则满足$\frac{x_1}{x_3}=x,\frac{x_2}{x_3}=y$的三数$x_1,x_2,x_3$，其中$(x3≠0)$叫做点$p$的齐次(笛氏)坐标，记作$p(x_1,x_2,x_3); (x,y)$叫做点$p$的非齐次坐标。

如：点(2, 4, -1) 的非齐次坐标为(-2, -4)，反之也成立。

现在说明，$(x_1, x_2, 0)$可以作 为无穷远点的坐标

证明：

设直线

$y= \lambda x+b$

如果在 (1) 里 b 变动，而 a 不变，则 (1) 表示一组平行直线。

现在取 (1) 里一定直线$l$，即$\lambda, b$均为定值，$l$上一点$p$的非齐次坐标为$(x, \lambda x+b)$， 其齐次坐标为$(x, \lambda x+b, 1)$或$(1, \lambda + \frac{b}{x}, \frac{1}{x})$.当p从$l$上的两个方向趋于无穷远时，即当$x→+∞$或$x→-∞$时得点$p$的齐次坐标的极限为$(1, \lambda, 0)$ 即$(1, \lambda + \frac{b}{x}, \frac{1}{x} \to (1, \lambda, 0)$，这是与b无关的一组数。因此，可以规定以$\lambda$为决定的方向的无穷远点的无数组齐次坐标为$(p, p\lambda, 0)$ (其中$\lambda≠0$)，于是直线$y= \lambda x+ b$上的无穷远点的坐标为$(1, \lambda, 0)$。

三重积

三重积，又称混合积，是三个向量相乘的结果。向量空间中，有两种方法将三个向量相乘，得到三重积，分别称作标量三重积和向量三重积。

正交矩阵

如果$AA^T=E$（$E$为单位矩阵，$A^T$表示“矩阵A的转置矩阵”）或$A^TA=E$，则n阶实矩阵A称为正交矩阵。

学过矩阵理论或者线性代数的肯定知道**正交矩阵（orthogonal matrix）**是一个非常好的矩阵，为什么这么说？原因有一下几点：

1. 正交矩阵每一列都是单位矩阵，并且两两正交。最简单的正交矩阵就是单位阵。
2. 正交矩阵的逆（inverse）等于正交矩阵的转置（transpose）。同时可以推论出正交矩阵的行列式的值肯定为正负1的。
3. 正交矩阵满足很多矩阵性质，比如可以相似于对角矩阵等等。

以上可以看出正交矩阵是非常特殊的矩阵，而本文题目中的旋转矩阵就是一种正交矩阵！它完美的诠释了正交矩阵的所有特点。

证明旋转矩阵是正交矩阵

https://www.cnblogs.com/caster99/p/4703033.html

SVD

https://zhuanlan.zhihu.com/p/29846048

SVD也是对矩阵进行分解，但是和特征分解不同，SVD并不要求要分解的矩阵为方阵。假设我们的矩阵A是一个m×n的矩阵，那么我们定义矩阵A的SVD为：

$A = U\Sigma V^T$

其中$U$是一个$m\times m$的矩阵，$\Sigma$是一个$m\times n$的矩阵，除了主对角线上的元素以外全为0，主对角线上的每个元素都称为奇异值， $V$是一个$n\times n$的矩阵。 $U$、$V$都是酉矩阵，即满足$U^TU=I, V^TV=I$。下图可以很形象的看出上面SVD的定义：

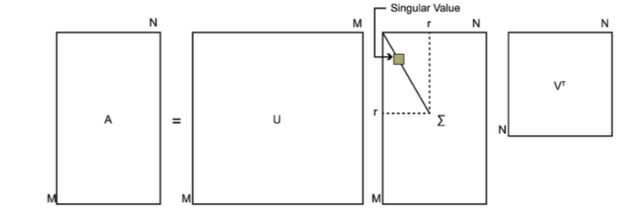
求SVD分解后的三个矩阵：

如果我们将A的转置和A做矩阵乘法，那么会得到n×n的一个方阵$A^TA$ 。既然$A^TA$是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式：

$(A^TA)v_i=\lambda_i v_i$

这样我们就可以得到矩阵$A^TA$的n个特征值和对应的n个特征向量v了。将$A^TA$的所有特征向量张成一个n×n的矩阵V，就是我们SVD公式里面的V矩阵了。一般我们将V中的每个特征向量叫做A的右奇异向量。

如果我们将A和A的转置做矩阵乘法，那么会得到m×m的一个方阵$AA^T$。既然$AA^T$是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式：

$(AA^T)u_i=\lambda_iu_i$

这样我们就可以得到矩阵$AA^T$的m个特征值和对应的m个特征向量u了。将 $AA^T$的所有特征向量张成一个m×m的矩阵U，就是我们SVD公式里面的U矩阵了。一般我们将U中的每个特征向量叫做A的左奇异向量。

U和V我们都求出来了，现在就剩下奇异值矩阵Σ没有求出了。

由于Σ除了对角线上是奇异值其他位置都是0，那我们只需要求出每个奇异值σ就可以了。

我们注意到:

$A=U\Sigma V^T \Rightarrow AV =U\Sigma V^TV \Rightarrow AV=U\Sigma \Rightarrow Av_i=\sigma_iu_i \Rightarrow \sigma_i=Av_i/u_i$

这样我们可以求出我们的每个奇异值，进而求出奇异值矩阵Σ。

上面还有一个问题没有讲，就是我们说$A^TA$的特征向量组成的就是我们SVD中的V矩阵，而$A^TA$的特征向量组成的就是我们SVD中的U矩阵，这有什么根据吗？这个其实很容易证明，我们以V矩阵的证明为例。

$A=U\Sigma V^T \Rightarrow A^T = V\Sigma U^T\Rightarrow A^TA=V\Sigma U^TU\Sigma V^T = V \Sigma^2V^T$

上式证明使用了$U^U=I, \Sigma^T=\Sigma$。可以看出$A^TA$的特征向量组成的的确就是我们SVD中的V矩阵。类似的方法可以得到$AA^T$的特征向量组成的就是我们SVD中的U矩阵。

进一步我们还可以看出我们的特征值矩阵等于奇异值矩阵的平方，也就是说特征值和奇异值满足如下关系：

$\sigma_i=\sqrt \lambda_i$

这样也就是说，我们可以不用 $\sigma_i = \dfrac{Av_i}{u_i}$ 来计算奇异值，也可以通过求出 $A^TA$ 的特征值取平方根来求奇异值。

SVD一些形式

参考： 《机器学习实践》第十四章 ——Peter Harrington

对于奇异值,它跟我们特征分解中的特征值类似，在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。

也就是说，我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。

也就是说：

$A_{m\times n}=U_{m\times m}\Sigma_{m\times n}V^T_{n\times n}\approx U_{m\times k}\Sigma_{k\times k}V^T_{k\times n}$

其中k要比n小很多，也就是一个大的矩阵A可以用三个小的矩阵 $U_{m\times k}, \Sigma_{k\times k}, V^T_{k\times n}$ 来表示。如下图所示，现在我们的矩阵A只需要灰色的部分的三个小矩阵就可以近似描述了。

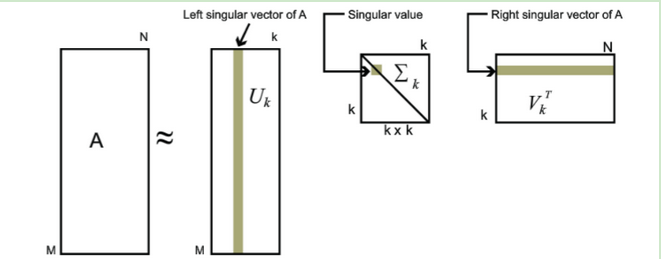
由于这个重要的性质，SVD可以用于PCA降维，来做数据压缩和去噪。也可以用于推荐算法，将用户和喜好对应的矩阵做特征分解，进而得到隐含的用户需求来做推荐。同时也可以用于NLP中的算法，比如潜在语义索引（LSI）。

共轭转置

参考：百度百科-共轭转置

共轭就是矩阵每个元素都取共轭（实部不变，虚部取负）。

转置就是把矩阵的每个元素按左上到右下的所有元素对称调换过来。

共轭转置就是先取共轭，再取转置。

以复数为元素的矩阵，其共轭矩阵指对每一个元素取共轭之后得到的矩阵。

共轭矩阵又称Hermite阵，每一个第i行第j列的元素都与第j行第i列的元素的共轭相等。

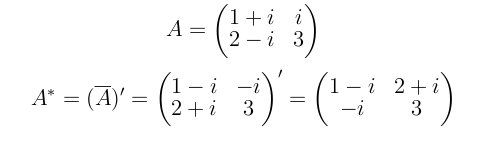
斜对称矩阵

设M是方阵， 如果它的转置$M^T$加上它本身恰好是零矩阵，那么就称M是斜对称矩阵。斜对称矩阵也可以称为反对称矩阵或交错矩阵。斜对称矩阵具有性质：数域P上的斜对称矩阵的主对角元全是零；数域P上的n级斜对称矩阵A，如果n是奇数，则|A|=0，因此数域P上的奇数级斜对称矩阵一定是奇异的（即不可逆的）。

即$A=-A^T$。